Review of ∆ and Γ hedging
∆ hedging
Recall the Delta of a portfolio Πt = Π(t, St) is the rate of change of its value with respect to the price of the underlying asset St:
∆t = ∆t(Π) := ∂SΠ(t, St).
∆-hedging involves creating a delta-neutral position: ∆t(Π) = 0.
Since the delta of the underlying is simply 1, can ∆-neutralize an initial position Π0 by adding “−∆t(Π0)” in the underlying asset.
Γ hedging
Recall the Gamma of a portfolio Πt = Π(t, St) is the rate of change of the delta ∆t = ∆(t, St) with respect to the underlying:
Γ-hedging involves creating a gamma-neutral position: Γt(Π) = 0.
Since gamma of the underlying is 0, can Γ-neutralize a position Π0 by adding “−∆t(Π0)” in the underlying asset, giving new position Π1.
However, moving from Π0 to Π1 can destroy delta neutrality (if any).
Trick: find yet another instrument with delta “−∆t(Π1)” but with zero gamma to add to the portfolio to arrive at Π2 that is ∆ and Γ neutral.
WARNING: Not always feasible to maintain Γ neutrality.
PnL of ∆-hedged position
Theta as a proxy for Gamma
Recall value f = f(t, S) of a call satisfies BSM PDE


This relationship between the Gamma and Theta of an option is fundamental for making money with options.
Infinitesimal rebalancing PnL governed by Γ
Consider the infinitesimal PnL of a portfolio consisting only of a call:

where σreal is realized volatility.
In contrast, Greeks Θt, Γt, ∆t computed at implied vol σimp
Putting everything together, the hedged position
Π(t, St) := f(t, St) − ∆tSt,
exhibits the “infinitesimal rebalancing PnL” (see Sinclair [4])

Infinitesimal PnL governed by Gamma and Vega
Can take step further with movement σimp → σ′imp of implied vol.
Writing ∆-hedged position Πt = Π(t, St, σimp),

where Vt = ∂σf(t, St, σimp) is the vega of the call.
Can take σ′imp ≈ σreal (market will match realized vol to some degree)
Thus, a goal of options trading: identify “volatility mismatches” so
- Long Gamma/Vega makes money if σreal > σimp ⋆
- Short Gamma/Vega makes money if σimp > σreal ⋆
Summary: can make money with hedged position from discrepancies in either realized or implied volatilities.
Correlation of spot and vol: hedging vega with delta
Relationship between smile and spot correlation with vol
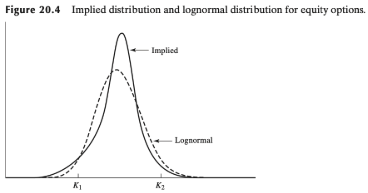
Negative correlation of prices and vol corresponds to heavy left tail and thin right tail of implied distribution of ST; this is because
- if S ↓ accompanied by σ ↑, then greater declines more likely
- if S ↑ accompanied by σ ↓, then greater increases less likely
Accordingly, the smile will have a negative skew (slope).
Positive correlation of prices and vol corresponds to thin left tail and heavy right tail of implied distribution of ST; this is because
- if S ↓ and σ ↓ together, then greater declines become less likely
- if S ↑ and σ ↑ together, then greater increases more likely
Accordingly, the smile will have a positive skew (slope).
Illustration of negative correlation of spot and vol (Hull, [3])
Correlation of vol and spot in cryptocurrencies
In crypto, strong linear relationship between spot and vol observed in options with longer tenors (e.g., fix 182 days to maturity)
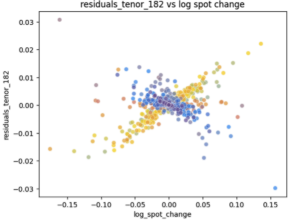
Calculate deltas that fixed strike has yesterday for each tenor Predicted strike: one with same delta as fixed strike had yesterday y-axis is difference between predicted and true vols wrt strikes. Darker colors = more recent…appears to exhibit regime switching!
Correlation of vol and spot in cryptocurrencies
Such structure forms with tenors as small as 14 (or even 7) days:

Instruments used for Hedging in crypto derivatives
Note transactions have to go through the blockchain. Consequently, it is VERY expensive to transact. Potential solution: create a Futures Market.
- Typically a complex, exchange dependent settlement procedure:
- Perpetual Future is VERY unique to the crypto market.
- There is opportunity for crypto carry trade!!
- There is term structure that is not necessarily consistent
Inconsistent term structure
Key Takeaway
There is a particular interaction between vega and delta in crypto. This interaction is atypical, so money can be made!
Vega hedging
Model Driven Vega Hedging
Vega hedging: closing vega risk at one strike using a different one.
– Standard in equities, which employ stochastic vol models
As people say (see Gatheral [2]), “options are hedged with options.”
More precisely, recall prototypical two factor stochastic vol model:
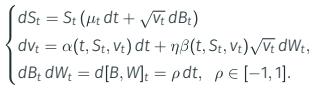
Issue: two sources of randomness to deal with for BSM argument
Set up portfolio Π = V − ∆S − ∆1V1 of two options V, V1, so that
main option V = V(t, S, v) hedged with auxiliary option V1 = V1 (t, S, v).
1. Delta hedge: ∂SV − ∆1∂SV1 − ∆ = 0 (eliminate dS noise)
2. Vega hedge: ∂vV − ∆1∂vV1 = 0 (eliminate dv noise)
Application of Ito’s confirms riskless position: dΠ = rΠ dt.
Valuation equation
Argument of previous slide leads to valuation equation for
V = V(t, S, v) analogous to BSM PDE:
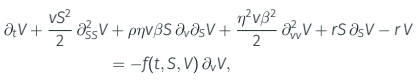
for some function f, usually written as
where ϕ = ϕ(t, S, V) is “market price of volatility risk”
(and we recall α, β are drift and volatility factor for variance).
Delta hedging with stochastic vol
The delta from a stochastic volatility model implies a type of
correlation between vol and spot!!
Recall a few well known facts:
- If ρ = 0, then any stochastic vol model implies “sticky delta”.
- If model is mainly local vol, then delta is mostly “sticky strike.”
Crypto lives in the middle of these:
- Short term vols are mostly sticky delta
- Low delta strikes are mostly sticky strike
- Interestingly tends to be the case that ρ > 0
- recall ρ controls the skew of the surface
- thus can have positive volatility skew as argued before
In general impossible to fit stochastic vol model well to market.
Accordingly, we resort to some tricks…
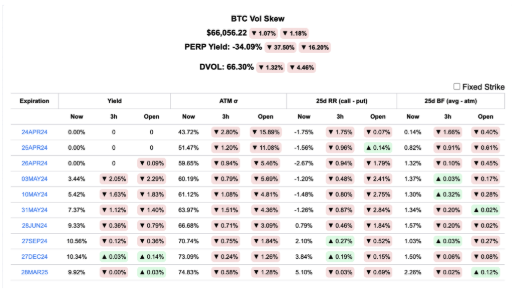
Example of vol. surface in BTC
There is a particular interaction between vega and delta in crypto. This interaction is atypical, so money can be made!
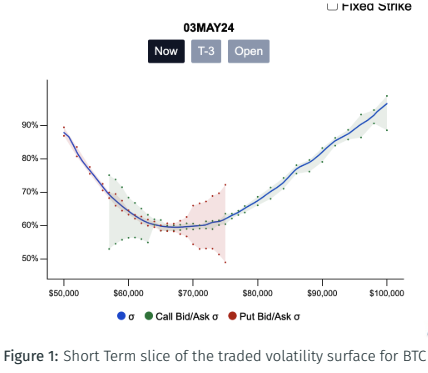
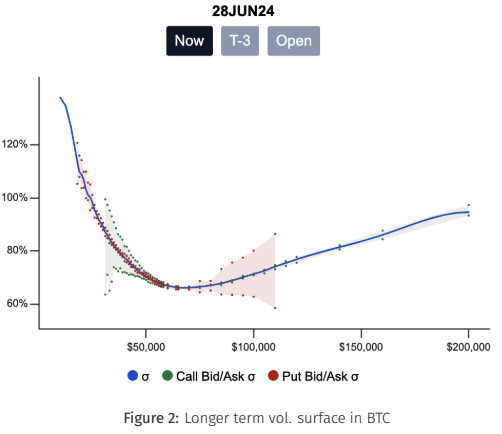
Statistical Vega Hedging
Do a dimensionality reduction of the term structure on a surface to
ideally project all the risks at different tenors, to a single one.
At Arbelos, we use 3 PCA’s to do so:
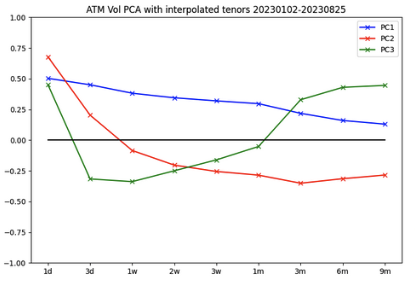
Optimal execution and nonlinear price impact
Optimization problem for optimal execution
Rebalancing to preserve ∆ and Γ neutrality requires making trades
Such trades can have adverse effect on market microstructure
Must trade in careful way (say, liquidate for concreteness)
Following Ch.8 of Cartea, Jaimungal, Penalva [1], agent optimizes
over admissible controls A, subject to dynamical constraint
where:

Optimal execution
Approximation with T >> 0 is to take premium or depth δ to be


Note this formula assumes a linear penalty and linear price impact.
Illustration of Price Impact (Ch.6, Cartea, Jaimungal, Penalva [1])
Price impact can sometimes be reasonably modelled linearly:

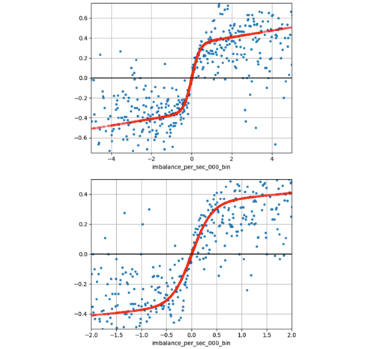
Issues with price impact in crypto
But graphs of imbalance clearly shows nonlinear price impact!
References
Á. Cartea, S. Jaimungal, and J. Penalva.
Algorithmic and high-frequency trading.
Cambridge University Press, 2015.
J. Gatheral.
The volatility surface: a practitioner’s guide.
John Wiley & Sons, 2011.
J. C. Hull.
Options, futures, and other derivatives.
Pearson Education, 2022.
E. Sinclair.
Positional Option Trading: An Advanced Guide.
John Wiley & Sons, 2020.
Case study of an exotic structure: One Touch
Terminology
Consider problem of pricing a contingent claim with payoff
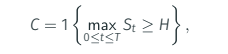
i.e., an American Binary Call with barrier H or one-touch.
In Black-Scholes, “dynamic hedging” refers to continuously trading.
By contrast, “static hedging” refers to discretely many trades.
– For our purposes, usually consists of at most two trades.
Symmetric Case
Suppose the price process St is Brownian motion: dSt = σ dBt.
Then the distribution of ST will be symmetric in the sense that
- upon hitting H, binaries with payoff 1{ST ≥ H} are worth $0.5.
But, upon hitting H, the one-touch will “knock-in” and pay $1.
Hence, at H, a one-touch is worth the same as 2 binaries.
Static replication strategy for one-touch in symmetric case:
- Buy two binary calls struck at H at inception t = 0.
- If price ever touches barrier H, dissolve portfolio to pocket $1.
Summary:
Driftless Case
Suppose St exhibits driftless log-normal dynamics with r − q = 0:
dSt = σ St dBt
Distribution of ST has weaker positive skew that must be corrected!
Symmetry to exploit: at S = H, d2 = −d1 since log(S/H) = 0.
Then value of a call with strike K = H at St = H is given by
StN(d1) − KN(d2) = H · [N(−d2) − N(d2)] = H · [1 − 2N(d2)].
But we know N(d2) is the value of a binary call struck at H.
Rearranging, this implies two binaries and 1/H calls all struck at H is exactly equal to $1 upon hitting the barrier H.
Thus, static replication strategy for one-touch in driftless case:
- Buy two binary calls and 1/H calls struck at H.
- If price ever touches barrier, dissolve portfolio to pocket $1.
Issue with General case
Suppose St exhibits more general log-normal dynamics:
Distribution of ST now has even more complicated skew!
Symmetry to exploit now much more complicated.
For example, put-call symmetry now involves exponent
Produces replication terms nonlinear in underlying (see next slide).
– This symmetry is now much less intuitive to work with.
– No finite portfolio of vanillas provides a perfect static hedge.
Solutions for General case
There is an elegant solution.
– But solution requires passing by some inelegant formulas.
One can check the analytic formula for a one-touch struck at H is
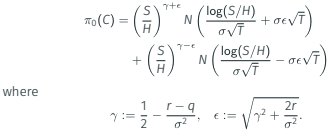
TRICK: Simply let T ↓ 0 here to find infinitesimal European payoff:
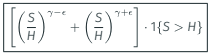
Reduces exactly to previous driftless case formula when r = q = 0.
Finite static hedge for General case
Unfortunately, as indicated, this last payoff features nonlinearities.
Solution: Settle for first order approximation of this formula:

PROS: Formula practically provides an approximate static hedging
strategy that is readily implemented and remembered.
CONS: Simple replicating portfolio will not give as accurate of a price
as PDE methods based on LSV models (forthcoming work).
Vega and skew in binaries
Just saw “one touches are roughly twice a binary plus a correction.”
To price a binary call, recall


Recall particular interaction between vega and delta in crypto
Aim to exploit this interaction here (forthcoming work).
